La historia de la trigonometría comienza con los Babilónicos y los Egipcios. Estos últimos establecieron la medida de los ángulos en grados, minutos y segundos. Sin embargo, en los tiempos de la Grecia clásica, en el siglo II a.C. el astrónomo Hiparco de Nicea construyó una tabla de cuerdas para resolver triángulos.
300 años después, el astrónomo Tolomeo utilizó r = 60, pues los griegos adoptaron el sistema numérico (base 60) de los babilonios.
El libro de astronomía el Almagesto, escrito por él, también tenía una tabla de cuerdas junto con la explicación de su método para compilarla, y a lo largo del libro dio ejemplos de cómo utilizar la tabla para calcular los elementos desconocidos de un triángulo a partir de los conocidos. El teorema de Menelao utilizado para resolver triángulos esféricos fue autoría de Tolomeo.
Al mismo tiempo, los astrónomos de la India habían desarrollado también un sistema trigonométrico basado en la función seno en vez de cuerdas como los griegos. Esta función seno, era la longitud del lado opuesto a un ángulo en un triángulo rectángulo de hipotenusa dada.
A finales del siglo VIII los astrónomos Árabes trabajaron con la función seno y a finales del siglo X ya habían completado la función seno y las otras cinco funciones. También descubrieron y demostraron teoremas fundamentales de la trigonometría tanto para triángulos planos como esféricos. Los matemáticos sugirieron el uso del valor r = 1.
A principios del siglo XVII, el matemático John Napier inventó los logaritmos y gracias a esto los cálculos trigonométricos recibieron un gran empuje.
A mediados del siglo XVII Isaac Newton inventó el cálculo diferencial e integral. Uno de los fundamentos del trabajo de Newton fue la representación de muchas funciones matemáticas utilizando series infinitas de potencias de la variable x. Newton encontró la serie para el sen x y series similares para el cos x y la tg x. Con la invención del cálculo las funciones trigonométricas fueron incorporadas al análisis, donde todavía hoy desempeñan un importante papel tanto en las matemáticas puras como en las aplicadas.
Por último, en el siglo XVIII, el matemático Leonhard Euler demostró que las propiedades de la trigonometría eran producto de la aritmética de los números complejos y además definió las funciones trigonométricas utilizando expresiones con exponenciales de números complejos.

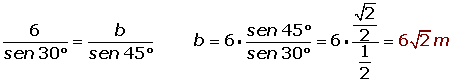
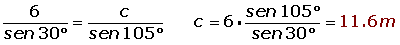
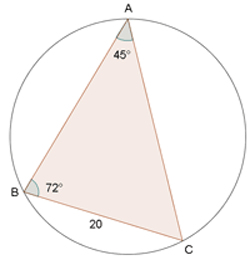
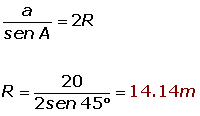

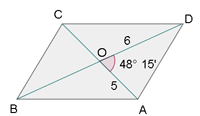

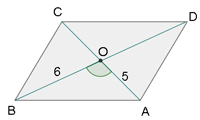
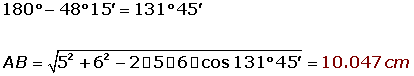








.jpg)