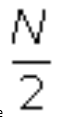REGLA DE LA ADICIÓN
Ejemplo 1: Se lanzan un dado. Usted gana $ 3000 pesos si el resultado es par ó divisible por tres ¿Cuál es la probabilidad de ganar ?
Lo que primero hacemos es definir los sucesos :
Sea A = resultado par : A = { 2, 4, 6 }
Sea B = resultado divisible por 3 : B = { 3, 6 } . Ambos sucesos tienen intersección ?
Ejemplo 2 : Se tiene una baraja de cartas ( 52 cartas sin jockers), ¿ Cuál es la probabilidad de sacar una Reina ó un As ?
Sea A = sacar una reina y sea B = sacar un as, entonces :
REGLA DE LA MULTIPLICACIÓN
1. (Inspección de Lotes)
Un lote contiene  items de los cuales
items de los cuales  son defectuosos. Los items son seleccionados uno despues del otro para ver si ellos son defectuosos. Suponga que dos items son seleccionados sin reemplazamiento(Significa que el objeto que se selecciona al azar se deja por fuera del lote). ¿ Cúal es la probabilidad de que los dos items seleccionados sean defectuosos?.
son defectuosos. Los items son seleccionados uno despues del otro para ver si ellos son defectuosos. Suponga que dos items son seleccionados sin reemplazamiento(Significa que el objeto que se selecciona al azar se deja por fuera del lote). ¿ Cúal es la probabilidad de que los dos items seleccionados sean defectuosos?.
 items de los cuales
items de los cuales  son defectuosos. Los items son seleccionados uno despues del otro para ver si ellos son defectuosos. Suponga que dos items son seleccionados sin reemplazamiento(Significa que el objeto que se selecciona al azar se deja por fuera del lote). ¿ Cúal es la probabilidad de que los dos items seleccionados sean defectuosos?.
son defectuosos. Los items son seleccionados uno despues del otro para ver si ellos son defectuosos. Suponga que dos items son seleccionados sin reemplazamiento(Significa que el objeto que se selecciona al azar se deja por fuera del lote). ¿ Cúal es la probabilidad de que los dos items seleccionados sean defectuosos?.
Solución
Sea los eventos

entonces dos items seleccionados seran defectuosos, cuando ocurre el evento  que es la intersección entre los eventos
que es la intersección entre los eventos  y
y  . De la información dada se tiene que:
. De la información dada se tiene que:
 que es la intersección entre los eventos
que es la intersección entre los eventos  y
y  . De la información dada se tiene que:
. De la información dada se tiene que:

así probabilidad de que los dos items seleccionados sean defectuosos es

Ahora suponga que selecciona un tercer item, entonces la probabilidad de que los tres items seleccionados sean defectuosos es



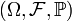 y dos eventos (o sucesos)
y dos eventos (o sucesos) 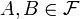 con
con 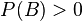 , la probabilidad condicional de A dado B está definida como:
, la probabilidad condicional de A dado B está definida como: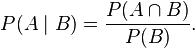











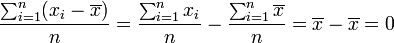
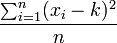 es mínimo cuando
es mínimo cuando  . Este resultado se conoce como Teorema de König. Esta propiedad permite interpretar uno de los parámetros de dispersión más importantes: la varianza.
. Este resultado se conoce como Teorema de König. Esta propiedad permite interpretar uno de los parámetros de dispersión más importantes: la varianza. entonces
entonces 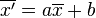 , donde
, donde 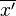 es la media aritmética de los
es la media aritmética de los 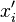 , para i = 1, ..., n y a y bnúmeros reales.
, para i = 1, ..., n y a y bnúmeros reales.