martes, 3 de junio de 2014

MEDIDAS DE TENDENCIA CENTRAL

La medidas de centralización nos indican en torno a qué valor (centro) se distribuyen los datos.

Media aritmética.
La media aritmética es el valor obtenido al sumar todos los datos y dividir el resultado entre el número total de datos.

\overline{x} = \frac{x_1 + x_2 + ... + x_n}{n} = \frac{\sum_{i=1}^n x_i}{n}

Propiedades

Las principales propiedades de la media aritmética son:
  • Su cálculo es muy sencillo y en él intervienen todos los datos.
  • Su valor es único para una serie de datos dada.
  • Se usa con frecuencia para comparar poblaciones, aunque es más apropiado acompañarla de una medida de dispersión.
  • Se interpreta como "punto de equilibrio" o "centro de masas" del conjunto de datos, ya que tiene la propiedad de equilibrar las desviaciones de los datos respecto de su propio valor:
\frac{\sum_{i=1}^n (x_i-\overline{x})}{n} = \frac{\sum_{i=1}^n x_i}{n} - \frac{\sum_{i=1}^n \overline{x}}{n} = \overline{x} - \overline{x} = 0
  • Minimiza las desviaciones cuadráticas de los datos respecto de cualquier valor prefijado, esto es, el valor de 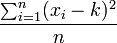 \frac{\sum_{i=1}^n (x_i-k)^2}{n} es mínimo cuando k = \overline{x}. Este resultado se conoce como Teorema de König. Esta propiedad permite interpretar uno de los parámetros de dispersión más importantes: la varianza.
  • Se ve afectada por transformaciones afines (cambios de origen y escala), esto es, si
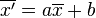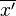x_i' = ax_i+b entonces \overline{x'} = a \overline{x} + b, donde \overline{x'} es la media aritmética de los 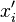x_i', para i = 1, ..., n y a y bnúmeros reales.

Mediana.

Es el valor que ocupa el lugar central de todos los datos cuando éstos están ordenados de menor a mayor.
La mediana se representa por Me.
La mediana se puede hallar sólo para variables cuantitativas.
Ordenamos los datos de menor a mayor.
Si la serie tiene un número impar de medidas la mediana es la puntuación central de la misma.
Si la serie tiene un número par de puntuaciones la mediana es la media entre las dos puntuaciones centrales.
La mediana se encuentra en el intervalo donde la frecuencia acumulada llega hasta la mitad de la suma de las frecuencias absolutas.
Es decir tenemos que buscar el intervalo en el que se encuentre
.

Moda.

La moda es el valor que tiene mayor frecuencia absoluta.
Se representa por Mo.
Se puede hallar la moda para variables cualitativas y cuantitativas.
Si en un grupo hay dos o varias puntuaciones con la misma frecuencia y esa frecuencia es la máxima, la distribución es bimodal o multimodal, es decir, tiene varias modas.
Cuando todas las puntuaciones de un grupo tienen la misma frecuencia, no hay moda.
Si dos puntuaciones adyacentes tienen la frecuencia máxima, la moda es el promedio de las dos puntuaciones adyacentes.
1º Todos los intervalos tienen la misma amplitud.



Publicado por en

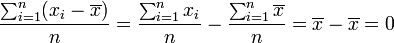
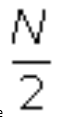
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)