Un polígono es una figura plana compuesta por una secuencia finita de segmentos rectos consecutivos que cierran una región en el plano. Estos segmentos son llamados lados, y los puntos en que se intersecan se llaman vértices.
El interior del polígono es llamado área. .
Un polígono está conformado por una línea poligonal, es decir, el conjunto ordenado de segmentos.
ELEMENTOS DE UN POLÍGONO
En un polígono se pueden distinguir los siguientes elementos geométricos:
-Lado (L): Es cada uno de los segmentos que conforman el polígono.
-Vértice (V): Es el punto de intersección (punto de unión) de dos lados consecutivos.
-Diagonal (d): Es el segmento que une dos vértices no consecutivos
-Perímetro (P): Es la suma de las longitudes de todos los lados del polígono.
-Semiperímetro (SP): Es la mitad del perímetro.
-Ángulo interior (AI): Es el ángulo formado internamente por dos lados consecutivos.
-Ángulo exterior (AE): Es el ángulo formado por un lado y la prolongación de un lado consecutivo.
Y SI ES REGULAR:
-Centro (C): Es el punto equidistante de todos los vértices y lados.
-Ángulo central (AC): Es el formado por dos segmentos de recta que parten del centro a los extremos de un lado.
-Apotema (a): Es el segmento que une el centro del polígono con el centro de un lado; es perpendicular a dicho lado.
-Diagonales totales  , en un polígono de
, en un polígono de  lados.
lados.
-Intersecciones de diagonales 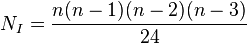 , en un polígono de
, en un polígono de  vértices.
vértices.
CLASIFICACIÓN:
Se pueden clasificar según:
-Numero de lados:
-Sus ángulos:
Cóncavos: Alguno de sus ángulos mide >180°
Convexos: Todos sus ángulos son <80°
-Su forma:
Regulares: Con todos sus lados y ángulos iguales
Irregulares: Con sus lados, angulos y diagonales desiguales.


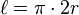





.jpg)







 , en un polígono de
, en un polígono de  lados.
lados.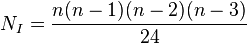 , en un polígono de
, en un polígono de 
