Existen dos teoremas de Thales de mileto:
Como definición previa al enunciado del teorema, es necesario establecer que dos triángulos son semejantes si tienen los ángulos correspondientes iguales y sus lados son proporcionales entre sí. El primer teorema de Tales recoge uno de los resultados más básicos de la geometría, al saber, que:
el primero nos habla acerca de la semejanza de triangulos y nos dice que:
"SI EN UN TRIANGULO SE TRAZA UNA LINEA PARALELA A CUALQUIERA DE SUS LADOS SE OBTIENE UN TRIANGULO SEMEJANTE AL TRIANGULO DADO."
Según parece, Tales descubrió el teorema mientras investigaba la condición de paralelismo entre dos rectas. De hecho, el primer teorema de Tales puede enunciarse como que la igualdad de los cocientes de los lados de dos triángulos no es condición suficiente de paralelismo. Sin embargo, la principal aplicación del teorema, y la razón de su fama, se deriva del establecimiento de la condición de semejanza de triángulos, a raíz de la cual se obtiene el siguiente corolario.
Si dos rectas cualesquieras se cortan por varias rectas paralelas, los segmentos determinados en una de las rectas son proporcionales a los segmentos correspondientes en la otra.





















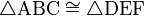




.png)
.jpg)

.jpg)










.jpg)


.jpg)


