La congruencia de triángulos estudia los casos en que dos o más triángulos presentan ángulos y lados de igual medida o congruentes.
Dos triángulos son congruentes si sus lados correspondientes tienen la misma longitud y sus ángulos correspondientes tienen la misma medida.
Si el triángulo ABC es congruente al triángulo DEF, la relación puede ser escrita matemáticamente así:
En muchos casos es suficiente establecer la igualdad entre tres partes correspondientes y usar uno de los siguientes criterios para deducir la congruencia de dos triángulos.
Criterios de congruencia de triángulos
Las condiciones mínimas que deben cumplir dos triángulos para que sean congruentes se denominan criterios de congruencia, los cuales son:
- Criterio LAL: Dos triángulos son congruentes si dos de sus lados tienen la misma longitud de sus homólogos, y el ángulo comprendido entre ellos tiene la misma medida de su homólogo.
- Criterio ALA: Si dos ángulos y el lado entre ellos son respectivamente congruentes con los mismos de otro triángulo, entonces los triángulos son congruentes.
- Criterio LLL: Si en dos triángulos los tres lados de uno son respectivamente congruentes con los del otro, entonces los triángulos son congruentes.
- Criterio LLA: Dos triángulos son congruentes si tienen respectivamente iguales dos lados y el ángulo opuesto al mayor de ellos.
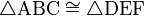




No hay comentarios:
Publicar un comentario